Macam - Macam Jilbab Modis dan anggun

Rumus-rumus Integral Baku

Fungsi Pangkat

Fungsi Eksponensial

Fungsi Trigonometri

*sumber : http://davidrevala.blogspot.com/2012/07/rumus-rumus-integral-baku.html*

INTEGRAL

RINGKASAN INTEGRAL.

Berikut ini adalah Tabel Integral dan beberapa teknik mengintegralkan.

Disini C adalah sembarang konstanta.

1.   Rumus umum

         

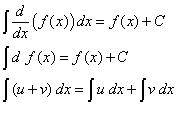
2.  Fungsi Aljabar

       

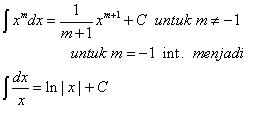
3.  Fungsi Eksponensial

      

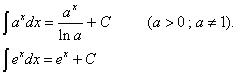
4.  Fungsi Trigonometri

     

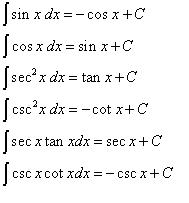
5.  Fungsi Trigonometri  (lanjutan)

    

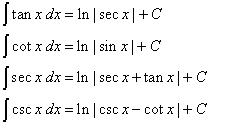
6.  Fungsi Invers Trigonometri

      

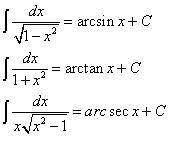
7.  Fungsi Hiperbolik

      

8.   Berikut ini adalah rumus-rumus trigonometri yang sering digunakan dalam menyelesaikan masalah integral.

      

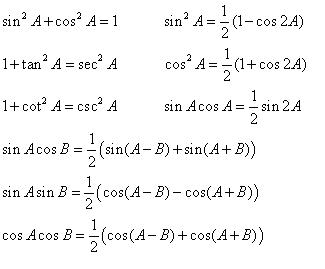
9.  Gunakan Rumus Trigonometri tersebut untuk mencari  

     

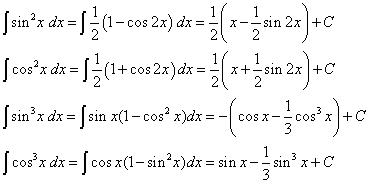
10.  Seperti nomor 9.

      

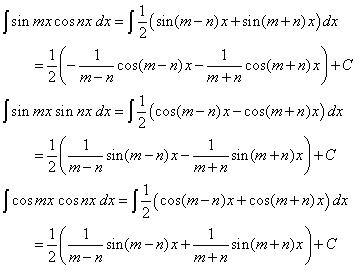
11.  INTEGRAL PARSIAL

      Rumus dari Integral Parsial

         

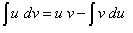
12.   Hitungan berikut menggunakan integral Parsial dengan cara reduksi

      

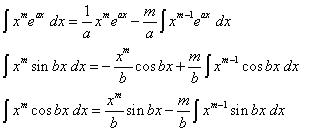
13.   Seperti nomor 12.

       

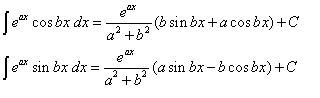
14.  Masih menggunakan integral parsial.

       

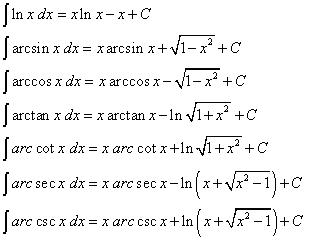
15.   Menyelesaikan masalah berikut menggunakan integral parsial,  dengan rumus reduksi

        

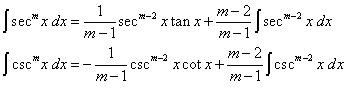
16.   SUBSTITUSI TERIGONOMETRI.

         Untuk Integrand dengan bentuk seperti berikut, gunakan substitusi Trigonometri

        

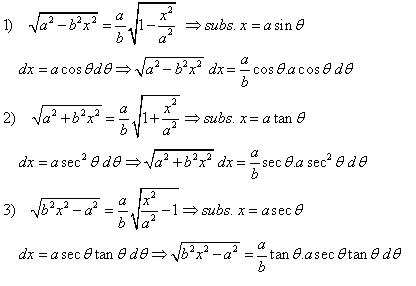
17.  INTEGRAL FUNGSI RASIONAL.

     

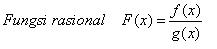
       Ubahlah fungsi rasional menjadi pecahan parsial, dengan cara :

      (i)    Apabila g (x) terdiri dari satu suku saja, bagilah  f (x) dengan g (x)

     (ii)  Apabila derajat f (x) lebih besar atau sama dengan derajat derajat g (x), bagilah f (x) dengan g (x) . Sisanya yang dipecah menjadi pecahan parsial.

   (iii)  Selanjutnya faktorkan penyebut, yaitu g (x).

   (iv)  Berikut adalah petunjuk mengubah ke pecahan parsial

        

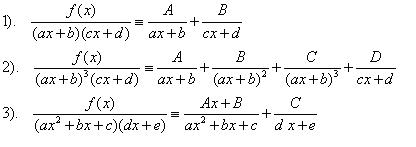
Catatan untuk  :

                           

          

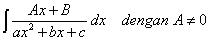
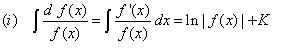
                     Integral fungsi rasional dengan pembilang adalah turunan penyebut sama dengan ln dari penyebut

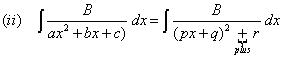            adalah bentuk arctan

             Contoh  :

                  

 

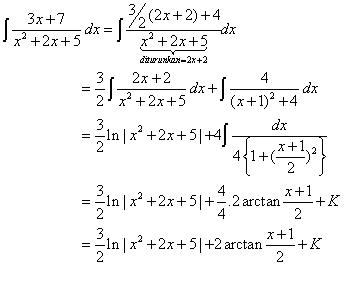
 *sumber : http://paulusharsono.wordpress.com/2009/06/09/integral/*

B. INTEGRAL TAK TENTU

Seperti yang telah kita ketahui bahwa integral merupakan antiturunan. Jadi, apabila terdapat fungsi F(x) yang dapat didiferensialkan pada interval [a, b] sedemikian hingga maka antiturunan dari f(x) adalah F(x) + c. Secara matematis, ditulis:

f(x) dx = F(x) + c
dimana	dx	=		Lambang integral yang menyatakan operasi antiturunan
	f(x)	=		Fungsi integran, yaitu fungsi yang dicari antiturunannya
	c	=		Konstanta

Sebagai contoh, dapat kita tuliskan:

karena

Sehingga kita dapat memandang integral tak tentu sebagai wakil keseluruhan keluarga fungsi (satu antiturunan untuk setiap nilai konstanta c). Pengertian tersebut dapat digunakan untuk membuktikan teorema-teorema berikut yang akan membantu dalam pengerjaan hitung integral.

Pembuktian Teorema 1

Pembuktian Teorema 3 dan 4

Contoh 1

Pembuktian Teorema 6

B.1. Aturan Integral Susbtitusi

Aturan integral substitusi seperti yang tertulis di Teorema 5. Aturan ini digunakan untuk memecahkan masalah pengintegralan yang tidak dapat diselesaikan dengan rumus-rumus dasar yang sudah dipelajari. Untuk lebih jelasnya, perhatikan contoh berikut ini.

Contoh 2

Contoh 3

Contoh 4

Pembuktian Teorema 7

Contoh 5

Contoh 6

Contoh 7

 

 *sumber ; http://www.ittelkom.ac.id/admisi/elearning/prog3.php?proses=1&kd=Mat-010102&bab=Integral&judul=Matematika&rincian=Integral%20Tak%20Tentu&kd_judul=Mat-01&kode_bab=01&kode_sub=02*